svm

发表于 | 分类于

支持向量机

分隔超平面为$w^Tx + b$
常数b类似于回归里的$w_0$

因为w为超平面的法向量，其中设距离为$\gamma$,$x_i 到x_0$的距离为$\gamma$,其中$x_0$为在平面的点，x为要求距离的点，

x的向量为$x_0 + \gamma \frac{w}{||w||}$ ,其中$\frac{w}{||w||}$为向量w的的单位向量，又有$w^Tx_0 + b = 0$与$w^Tw = ||w||^2$

$x-x_0 = \gamma \frac{\vec{w}}{||w||}$ 两边乘以$w^T$得

$w^T(x-x_0)= \gamma \frac{w^Tw}{||w||}$

$w^T(x-x_0)= \gamma \frac{||w||^2}{||w||}$

$w^Tx + b=\gamma||w||$

所以计算点A到平面的距离:值为$\frac{|w^TA + b| }{||w||}$

当$y_i$为1,-1时，$\gamma = \frac{2}{||w||}$ $s.t. w^Tx+b >= 1$

所以求$\gamma$的最大值，就是求$\frac{1}{2}||w||^2$ $s.t. w^Tx+b >= 1$的最小值

用拉格朗日乘子法来把约束条件加到求解方程里

$L(w,\alpha,b)=\frac{1}{2}||w||^2 + \sum\limits_{i=1}^m\alpha^i(1-y_i(w^Tx_i+b)$

令$\theta(w)=\mathop{max}\limits_{a_{i} >=0}L(w.\alpha,b)$

$\mathop{min}\limits_{w,b}\theta(w)=\mathop{min}\limits_{w,b}\mathop{max}\limits_{a_i >=0}L(w,\alpha,b)=p^*$

用对偶性，最大和最小互换，但是有kkt条件需要满足,才能保证$p^=d^$

$\mathop{max}\limits_{\alpha_i>=0}\mathop{mim}\limits_{w,b}L(w,\alpha,b)=d^*$

kkt条件为

min(f(x)),

$s.t. \\h_j(x)=0,j=1,2,..,p \\
g_k(x) <=0,k=1,2,…,q \\
x\in X\subset R^n
$

需要满足

  1. $L(w,\alpha,b)$对x求导为0
  2. $h_i(x)=0$
  3. $\alpha * g_k(x) =0$

对w,或b求导得到
$\frac{\partial L}{\partial w}=0 得到 w= \sum\limits_{i=1}^n\alpha_iy_ix_i$

$\frac{\partial L}{\partial b} =0 得到 \sum\limits_{i=1}^n\alpha_iy_i=0$

把w带回L中得到，一个只有$\alpha$的方程,??为什么是减去

$\mathop{max}\limits_{\alpha}\sum\limits_{i=1}^n\alpha_i - \frac{1}{2}\sum\limits_{i,j=1}^{n}\alpha_i\alpha_jy_iy_jx_i^Tx_j$

$s.t. \alpha_i >=0,i=1,2,…n, \\
\sum\limits_{i=1}^n\alpha_iy_i=0$

SMO内容

$\alpha$的部分

将方程变形，乘以-1,变成一个最小的问题

$\mathop{min}\limits_{\alpha}\frac{1}{2}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^n\alpha_i\alpha_jy_iy_jx_i^Tx_j -\sum\limits_{i=1}^n\alpha_i $

$s.t. \alpha_i >=0,i=1,2,…n, \\
\sum\limits_{i=1}^n\alpha_iy_i=0$

加入松弛变量C，保证可以有部分不是线性可分的，条件变为

$s.t. C>= \alpha_i >=0,i=1,2,…n, \\
\sum\limits_{i=1}^n\alpha_iy_i=0$

SMO为更新两个$\alpha$

则 $\alpha_1^{new}y_1 + \alpha_2^{new}y_2 = \alpha_1^{old}y_1 + \alpha_2^{old}y_2 = \zeta $

固定其他的值，只改变$\alpha_2^{new}的解$先确定它的上下限

$L<=\alpha_2^{new}<=H$

因为$C>=\alpha>=0$ 和$\alpha_1^{new}y_1 + \alpha_2^{new}y_2 = \alpha_1^{old}y_1 + \alpha_2^{old}y_2 = \zeta $

所以

当$y_1\ne y_2$时

$\alpha_1 - \alpha_2 = \zeta$

$\alpha_2 = \alpha_1 - \zeta$

得到

$C-\zeta>=\alpha_2 >= -\zeta$

结合$C>=\alpha>=0$,得到

$L=max(0,-\zeta),H=min(C,C-\zeta)$

同理，当$y_1=y_2$时，

$L=max(0,\zeta-C),H=min(C,\zeta)$

因此得到$\alpha_2^{new}$的上下界L和H为

$L=max(0,\alpha_2^{old}-\alpha_1^{old}),H=min(C,C+\alpha_2^{old} -\alpha_1^{old}),ify_1\ne y_2$

$L=max(0,\alpha_2^{old}+\alpha_1^{old}-C),H=min(C,\alpha_2^{old} +\alpha_1^{old}),ify_1= y_2$

固定除了$\alpha_1 \alpha_2的其他变量$

$w(\alpha_2) = \sum\limits_{i=1}^n\alpha_i - \frac{1}{2}\sum\limits_{i=1}^n\sum\limits_{i=1}^ny_iy_jx_i^Tx_j\alpha_i\alpha_j$

将$\alpha_1 \alpha_2$提出来得到

$w(\alpha_2) = \alpha_1 + \alpha_2 - \frac{1}{2}\alpha_1^2x_1^Tx_1 - \frac{1}{2}\alpha_2^2x_2^Tx_2 - y_1y_2\alpha_1\alpha_2x_1^Tx_2 - y_1\alpha_1v_1 - y_2\alpha_2v_2 + constant$

其中

定义$f(x_i) = \sum\limits_{j=1}^n\alpha_jy_jx_i^Tx_j + b$

$v_i =\sum\limits_{j=3}^n\alpha_jy_jx_i^Tx_j = f(x_i) -\sum\limits_{j=1}^2\alpha_jy_jx_i^Tx_j- b $

之后找到$\alpha_1和\alpha_2的关系$

因为$\sum\limits_{i=1}^n\alpha_iy_i=0$，所以将除了$\alpha_1y_1,\alpha_2y_2$的其他项看做常数-B

$\alpha_1y_1 + \alpha_2y_2 = B$，等式乘以$y_1$得到

$\alpha_1 = \gamma - s\alpha_2$ $，其中\gamma为By_1,s为y_1y_2$

带入公式，并且进行偏导

$\frac{\partial W(\alpha_2)}{\partial\alpha_2}=-s +1 +\gamma sx_1^Tx_1 - \alpha_2 x_1^Tx_1 - \alpha_2 x_2^Tx_2 - \gamma sx_1^Tx_2 + 2\alpha_2x_1^Tx_2 + y_2v_1 - y_2v_2 = 0$

导入$s=y_1y_2$得到

$\alpha_2^{new} = \frac{y_2(y_2-y_1+y_1\gamma(x_1^\intercal x_1 - x_1^\intercal x_2)+ v_1 -v_2)}{x_1^\intercal x_1 + x_2^\intercal x_2-2x_1^\intercal x_2}$

令$E_i = f(x_i)-y_i$

$\eta=x_1^Tx_1 + x_2^Tx_2 - 2x_1^Tx_2$

$E_i$为误差项，$\eta$为学习速率

已知$\gamma= \alpha_1^{old} + s\alpha_2^{old}$,和

$v_j=\sum\limits_{i=3}^n\alpha_iy_ix_j^Tx_i = f(x_j) -\sum\limits_{i=1}^2\alpha_iy_ix_j^Tx_i- b $$

简化$\alpha_2^{new}$

$\alpha_2^{new}=\alpha_2^{old} +\frac{y_2(E_1-E_2)}{\eta}$

加上约束，最终得到的解为

$\alpha_2^{new,clipped}=\begin{cases}
H,& \mbox{if }a_2^{new} >H \\
a_2^{new},& \mbox{if }L<=a_2^{new}<=H \\
L,& \mbox{if }a_2^{new} <L
\end{cases}$

又因为

$\alpha_1^{old}=\gamma -s\alpha_2^{old}$

$\alpha_1^{new} = \gamma -s\gamma_2^{new,clipped}$

消去$\gamma$得到

$\alpha_1^{new} = \alpha_1^{old} + y_1y_2(\alpha_2^{old} - \alpha_2^{new,clipped})$

b的部分

根据$y_1(w^Tx_1 + b)=1$两边乘以$y_1$，得到

$w^Tx_i+b =y_1$,又因为$w= \sum\limits_{i=1}^n\alpha_iy_ix_i$,得到

$\sum\limits_{i=1}^n\alpha_iy_ix_ix_1 +b=y1$单独提出$\alpha_1,alpha_2$，得

$b_1^{new} = y_1 -\sum\limits_{i=3}^n\alpha_iy_ix_i^Tx_1 - \alpha_1^{new}y_1x_1^Tx_1 - \alpha_2^{new}y_2x_2^Tx_1$

其中前两项为
$y_1 -\sum\limits_{i=3}^n\alpha_iy_ix_i^Tx_1=-E_1 + \alpha_1^{old}y_1x_1^Tx_1 + \alpha_2^{old}y_2x_2^Tx_1 + b^{old}$

整理得到

$b_1^{new}=b^{old} -E_1-y_1(\alpha_1^{new}- \alpha_1^{old})x_1^Tx_1 -y_2(\alpha_2^{new}-\alpha_2^{old})x_2^Tx_1$

同理得到$b_2^{new}$

$b_2^{new}=b^{old} -E_2-y_1(\alpha_1^{new}- \alpha_1^{old})x_1^Tx_2 -y_2(\alpha_2^{new}-\alpha_2^{old})x_2^Tx_2$

当$b_1,b_2都有效时，b^{new}=b_1^{new} = b_2^{new}$

所以，b的取值为

SMO计算梳理

  1. 计算误差$E_i$

$E_i=f(x_i) - y_i = \sum\limits_{j=1}^n\alpha_jy_jx_i^Tx_j +b -y_i$

  1. 计算上下限
  1. 计算$\eta$

$\eta=x_1^Tx_1 + x_2^Tx_2 - 2x_1^Tx_2$

  1. 更新$\alpha_j$

$\alpha_j^{new}=\alpha_j^{old} +\frac{y_j(E_1-E_j)}{\eta}$

  1. 根据取值范围修剪$\alpha_j$

$\alpha_j^{new,clipped}=\begin{cases}
H,& \mbox{if }a_j^{new} >H \\
a_2^{new},& \mbox{if }L<=a_j^{new}<=H \\
L,& \mbox{if }a_j^{new} <L
\end{cases}$

  1. 更新$\alpha_i$

$alpha_i^{new} = \alpha_i^{old} + y_jy_i(\alpha_j^{old} - \alpha_j^{new,clipped})$

  1. 更新$b_i,b_j$

$b_i^{new}=b^{old} -E_i-y_i(\alpha_i^{new}- \alpha_i^{old})x_i^Tx_i -y_j(\alpha_j^{new}-\alpha_j^{old})x_j^Tx_i$

$b_j^{new}=b^{old} -E_j-y_i(\alpha_i^{new}- \alpha_i^{old})x_i^Tx_j -y_j(\alpha_j^{new}-\alpha_j^{old})x_j^Tx_j$

  1. 根据bi,bj更新b
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import numpy as np
#SMO辅助函数
def loadDataset(file_name):
    """读取文件，得到两个list，
    data_mat 为2列m行，label_mat为m个元素"""
    data_mat=[];label_mat=[]
    fr = open(file_name)
    for line in fr.readlines():
        line_arr = line.strip().split('\t')
        data_mat.append([float(line_arr[0]),float(line_arr[1])])
        label_mat.append(float(line_arr[2]))
    return data_mat,label_mat

def selectJrand(i,m):
    """根据i，随机选取一个不是i的j"""
    import random
    j = i
    while(j==i):
        j = int(random.uniform(0,m))
    return j

def clipAlpha(aj,H,L):
    """修剪alpha"""
    if aj > H:
        aj = H
    elif aj < L:
        aj = L
    return aj
1
2
data_arr,label_arr = loadDataset('../../Downloads/machinelearninginaction/Ch06/testSet.txt')
len(data_arr)
100

1
set(label_arr)
{-1.0, 1.0}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
#流程为
#创建一个alpha向量，初始化为0
#当迭代次数小于最大迭代次数时(外循环)
#  对数据集的每一个数据向量(内循环)
#    如果该向量可以被优化:
#       随机选择另一个数据向量
#       同时优化这两个向量
#       如果两个向量都不能被优化，退出内循环
#  如果所有向量都没有被优化，增加迭代数目，继续下一次循环


def smo_simple(data_mat_in,class_labels,C,toler,max_iter):
    """数据集，数据标签，松弛常数，容错率，最大循环次数"""
    data_matrix = np.mat(data_mat_in);label_mat =np.mat(class_labels).transpose()
    b= 0;m,n = np.shape(data_matrix)
    alphas = np.mat(np.zeros((m,1)))
    iter = 0
    #外循环为总的循环数
    while(iter < max_iter):
        alpha_pairs_chanaged = 0
        #内循环为每个求E_i,判断是否要优化，能优化则随机找一个j，进行优化，优化成功则改变alpha_pairs_changed，
        #一次内循环后，如果有改变则改iter为0，继续进行，如果最大循环次数中都没有改变则跳出外循环，得到结果
        for i in range(m):
            #1.求E_i
            fx_i = float(np.multiply(alphas,label_mat).T * (data_matrix * data_matrix[i,:].T)) + b
            e_i = fx_i - float(label_mat[i])
            #根据kkt标准
            #alpha=0时，y_ig(x_i) >=1
            #0<alpha<C时，y_ig(x_i) = 1
            #alpha =C时，y_Ig(x_i) <= 1
            #如果不符合其中的一条，则进行优化
            if ((label_mat[i] * e_i < -toler) and (alphas[i] < C) or
               ((label_mat[i] * e_i > toler) and (alphas[i] > 0))):
                j = selectJrand(i,m)
                #求出了f(x_j)
                fx_j = float(np.multiply(alphas,label_mat).T * (data_matrix * data_matrix[j,:].T)) + b
                #fx_j = float(np.multiply(alphas,label_mat).T) * (data_matrix[j,:] * data_matrix.T).T + b #为原本方程的顺序
                e_j = fx_j - float(label_mat[j]) #得到E_j
                
                #2.求上下限
                alpha_i_old = alphas[i].copy()
                alpha_j_old = alphas[j].copy()
                if (label_mat[i] != label_mat[j]):
                    L = max(0,alphas[j] - alphas[i])
                    H = min(C,C+ alphas[j] - alphas[i])
                else:
                    L = max(0,alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L==H: #上下限相等，C为0，或者都为C，或者一个为C，一个为0；C为0时，则alpha都是0，不成立；都为C时，没法增大也没法变小，一个为C，一个为0时，即alpha_i为C，并不会改变，还是C
                    #print('L==H')
                    continue
                #eta与原本的符号相反
                eta = 2.0 * data_matrix[i,:] * data_matrix[j,:].T - data_matrix[i,:] * data_matrix[i,:].T - data_matrix[j,:] * data_matrix[j,:].T
                if eta >= 0: #变化率为负数，并不符合，eta应为正数
                    #print('eta >=0')
                    continue
                #原本的加上，现在为减去
                alphas[j] -= label_mat[j] *(e_i - e_j)/eta
                alphas[j] = clipAlpha(alphas[j],H,L)
                if (abs(alphas[j] - alpha_j_old) <0.00001):
                    #print('j not moving enough') #变化太小，跳出本次循环，换其他j
                    continue
                alphas[i] += label_mat[i]*label_mat[j] *(alpha_j_old - alphas[j])
                
                b_1 = b - e_i - label_mat[i] * (alphas[i] - alpha_i_old) * data_matrix[i,:] * data_matrix[i,:].T -  label_mat[j] * (alphas[j] - alpha_j_old)* data_matrix[i,:] * data_matrix[j,:].T
                
                b_2 = b - e_j - label_mat[i] * (alphas[i] -alpha_i_old) * data_matrix[i,:] * data_matrix[j,:].T - label_mat[j] * (alphas[j] - alpha_j_old) * data_matrix[j,:] * data_matrix[j,:].T
                if (0 <alphas[i]) and (C > alphas[i]): 
                    b = b_1
                elif (0 < alphas[j]) and (C > alphas[j]):
                    b = b_2
                else:
                    b = (b_1 + b_2) /2.0
                alpha_pairs_chanaged += 1
                #print('iter: %d i:%d,pairs changed %d'%(iter,i,alpha_pairs_chanaged))
                #print('alpha_i_old: %f, alpha_i_new: %f,alpha_j_old: %f, alpha_j_new: %f' %(alpha_i_old,alphas[i],alpha_j_old,alphas[j]))
        print("fullSet, iter: %d , pairs changed %d" % (iter,alpha_pairs_chanaged))
        if (alpha_pairs_chanaged == 0):
            iter += 1
        else:
            iter =0
        print('iteration number: %d' % iter)
    return b,alphas
1
b,alphas = smo_simple(data_arr,label_arr,0.6,0.001,10)
fullSet, iter: 0 , pairs changed 7
iteration number: 0
fullSet, iter: 0 , pairs changed 4
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 6
iteration number: 0
fullSet, iter: 0 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 2
iteration number: 0
fullSet, iter: 0 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 0
iteration number: 3
fullSet, iter: 3 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 0
iteration number: 3
fullSet, iter: 3 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 2
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 2
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 0
iteration number: 3
fullSet, iter: 3 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 0
iteration number: 3
fullSet, iter: 3 , pairs changed 0
iteration number: 4
fullSet, iter: 4 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 0
iteration number: 3
fullSet, iter: 3 , pairs changed 2
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 0
iteration number: 3
fullSet, iter: 3 , pairs changed 0
iteration number: 4
fullSet, iter: 4 , pairs changed 0
iteration number: 5
fullSet, iter: 5 , pairs changed 0
iteration number: 6
fullSet, iter: 6 , pairs changed 0
iteration number: 7
fullSet, iter: 7 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 0
iteration number: 3
fullSet, iter: 3 , pairs changed 0
iteration number: 4
fullSet, iter: 4 , pairs changed 0
iteration number: 5
fullSet, iter: 5 , pairs changed 0
iteration number: 6
fullSet, iter: 6 , pairs changed 0
iteration number: 7
fullSet, iter: 7 , pairs changed 0
iteration number: 8
fullSet, iter: 8 , pairs changed 0
iteration number: 9
fullSet, iter: 9 , pairs changed 0
iteration number: 10

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
#边界上的样本对应的α_i=0或者α_i=C，在优化过程中很难变化，然而非边界样本0<α_i<C会随着对其他变量的优化会有大的变化
from numpy import *
class optStruct:
    def __init__(self,dataMatIn, classLabels, C, toler):  # Initialize the structure with the parameters 
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = shape(dataMatIn)[0]
        self.alphas = mat(zeros((self.m,1)))
        self.b = 0
        self.eCache = mat(zeros((self.m,2))) #第一项储存是否有效
        
def calcEk(oS, k):
    fXk = float(multiply(oS.alphas,oS.labelMat).T*(oS.X*oS.X[k,:].T)) + oS.b
    Ek = fXk - float(oS.labelMat[k])
    return Ek
        
def selectJ(i, oS, Ei):         #this is the second choice -heurstic, and calcs Ej
    maxK = -1; maxDeltaE = 0; Ej = 0
    oS.eCache[i] = [1,Ei]  #set valid #choose the alpha that gives the maximum delta E
    validEcacheList = nonzero(oS.eCache[:,0].A)[0]
    if (len(validEcacheList)) > 1:
        for k in validEcacheList:   #loop through valid Ecache values and find the one that maximizes delta E
            if k == i: continue #don't calc for i, waste of time
            Ek = calcEk(oS, k)
            deltaE = abs(Ei - Ek)
            if (deltaE > maxDeltaE):
                maxK = k; maxDeltaE = deltaE; Ej = Ek
        return maxK, Ej
    else:   #in this case (first time around) we don't have any valid eCache values
        j = selectJrand(i, oS.m)
        Ej = calcEk(oS, j)
    return j, Ej

def updateEk(oS, k):#after any alpha has changed update the new value in the cache
    Ek = calcEk(oS, k)
    oS.eCache[k] = [1,Ek]
        
def innerL(i, oS):
    Ei = calcEk(oS, i)
    #判断是否可以优化，不可以直接返回0，
    #可以优化则搜索j，第一次是随机的，并且添加0到临时e表里，因为只有一个数值，所以随机选择j
    #之后更新alpah-i j对，更新i,j的e值，返回结果
    #第二次进入内训，i=1,添加1到临时表，j因为有两个所以选j=0，
    #一遍循环后临时e表都有了，之后就能按照alpah不是0的来选择最佳的j
    if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
        j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand
        alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
        if (oS.labelMat[i] != oS.labelMat[j]):
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L==H: 
            #print("L==H")
            return 0
        eta = 2.0 * oS.X[i,:]*oS.X[j,:].T - oS.X[i,:]*oS.X[i,:].T - oS.X[j,:]*oS.X[j,:].T
        if eta >= 0: 
            #print("eta>=0")
            return 0
        oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
        oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
        #因为alpha_j改变了，所以需要重新计算，为什么不是一起更新
        updateEk(oS, j) #added this for the Ecache
        if (abs(oS.alphas[j] - alphaJold) < 0.00001): 
            #print("j not moving enough")
            return 0
        oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j
        updateEk(oS, i) #added this for the Ecache                    #the update is in the oppostie direction
        b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[i,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[i,:]*oS.X[j,:].T
        b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[j,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[j,:]*oS.X[j,:].T
        if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
        elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
        else: oS.b = (b1 + b2)/2.0
        return 1
    else: return 0
def innerL1(i, oS): #一起更新临时e
    Ei = calcEk(oS, i)
    #判断是否可以优化，不可以直接返回0，
    #可以优化则搜索j，第一次是随机的，并且添加0到临时e表里，因为只有一个数值，所以随机选择j
    #之后更新alpah-i j对，更新i,j的e值，返回结果
    #第二次进入内训，i=1,添加1到临时表，j因为有两个所以选j=0，
    #一遍循环后临时e表都有了，之后就能按照alpah不是0的来选择最佳的j
    if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
        j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand
        alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
        if (oS.labelMat[i] != oS.labelMat[j]):
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L==H: 
            #print("L==H")
            return 0
        eta = 2.0 * oS.X[i,:]*oS.X[j,:].T - oS.X[i,:]*oS.X[i,:].T - oS.X[j,:]*oS.X[j,:].T
        if eta >= 0: 
            #print("eta>=0"); 
            return 0
        oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
        oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
        if (abs(oS.alphas[j] - alphaJold) < 0.00001): 
            #print("j not moving enough")
            return 0
        oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j
        updateEk(oS,j)
        updateEk(oS, i) #added this for the Ecache                    #the update is in the oppostie direction
        b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[i,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[i,:]*oS.X[j,:].T
        b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[j,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[j,:]*oS.X[j,:].T
        if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
        elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
        else: oS.b = (b1 + b2)/2.0
        return 1
    else: return 0
def smoP(dataMatIn, classLabels, C, toler, maxIter):    #full Platt SMO
    oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler)
    iter = 0
    entireSet = True; alphaPairsChanged = 0
    #当循环数不满时并且是循环整个数据集或者不是循环整个数据集但是有alpha对改变时
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged = 0
        if entireSet:   #go over all
            for i in range(oS.m):        
                alphaPairsChanged += innerL(i,oS)
                #print("fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
            print("fullSet, iter: %d , pairs changed %d" % (iter,alphaPairsChanged))
            iter += 1
        else:#go over non-bound (railed) alphas
            nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            for i in nonBoundIs:
                alphaPairsChanged += innerL(i,oS)
                #print("non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
            print("non-bound, iter: %d , pairs changed %d" % (iter,alphaPairsChanged))
            iter += 1
        #第一次循环为整个，循环后改变为循环non-bound，如果没有a对改变，则变成整个的数据集
        #在整个数据集循环后没有a对改变时，跳出循环，结束
        if entireSet: entireSet = False #toggle entire set loop
        elif (alphaPairsChanged == 0): entireSet = True  
        print("iteration number: %d" % iter)
    return oS.b,oS.alphas
1
data_arr, label_arr = loadDataset('../../Downloads/machinelearninginaction/Ch06/testSet.txt')
1
b, alphas = smoP(data_arr,label_arr,0.6,0.001,40)
fullSet, iter: 0 , pairs changed 6
iteration number: 1
non-bound, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 0
iteration number: 3

$w = \sum\limits_{i=1}^m\alpha_iy_ix_i$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#计算w值
def calc_ws(alphas,data_arr,class_labels):
    x = np.mat(data_arr)
    label_mat = np.mat(class_labels).transpose()
    m,n = np.shape(x)
    w = np.zeros((n,1))
    for i in range(m):
        w += np.multiply(alphas[i] * label_mat[i], x[i,:].T)
    return w

def calc_ws(alphas,data_arr,class_labels):
    #向量来求解
    x = np.mat(data_arr);label_mat = np.mat(class_labels).T
    w = x.T * np.multiply(alphas,label_mat) 
    return w
1
calc_ws(alphas,data_arr,label_arr)
matrix([[ 0.65307162],
        [-0.17196128]])

1
calc_ws(alphas,data_arr,label_arr)
matrix([[ 0.65307162],
        [-0.17196128]])

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#绘制样本
def showClassifer(dataMat, w, b):
    #绘制样本点
    data_plus = []                                  #正样本
    data_minus = []                                 #负样本
    for i in range(len(dataMat)):
        if label_arr[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    data_plus_np = np.array(data_plus)              #转换为numpy矩阵
    data_minus_np = np.array(data_minus)            #转换为numpy矩阵
    plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7)   #正样本散点图
    plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1], s=30, alpha=0.7) #负样本散点图
    #绘制直线
    x1 = max(dataMat)[0]
    x2 = min(dataMat)[0]
    a1, a2 = w
    b = float(b)
    a1 = float(a1[0])
    a2 = float(a2[0])
    y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2
    plt.plot([x1, x2], [y1, y2])
    #找出支持向量点
    for i, alpha in enumerate(alphas):
        if abs(alpha) > 0:
            x, y = dataMat[i]
            plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
    plt.show()
1
2
from matplotlib import pylab as plt
%matplotlib inline

c越高，说明越不能容忍出现误差,容易过拟合。C越小，容易欠拟合。C过大或过小，泛化能力变差

1
2
3
b, alphas = smo_simple(data_arr,label_arr,0.6,0.001,10)
ws = calc_ws(alphas,data_arr,label_arr)
showClassifer(data_arr,ws,b)
fullSet, iter: 0 , pairs changed 3
iteration number: 0
fullSet, iter: 0 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 4
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 3
iteration number: 0
fullSet, iter: 0 , pairs changed 2
iteration number: 0
fullSet, iter: 0 , pairs changed 2
iteration number: 0
fullSet, iter: 0 , pairs changed 4
iteration number: 0
fullSet, iter: 0 , pairs changed 3
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 3
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 0
iteration number: 3
fullSet, iter: 3 , pairs changed 0
iteration number: 4
fullSet, iter: 4 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 2
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 2
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 0
iteration number: 3
fullSet, iter: 3 , pairs changed 0
iteration number: 4
fullSet, iter: 4 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 0
iteration number: 3
fullSet, iter: 3 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 0
iteration number: 3
fullSet, iter: 3 , pairs changed 2
iteration number: 0
fullSet, iter: 0 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 0
iteration number: 3
fullSet, iter: 3 , pairs changed 0
iteration number: 4
fullSet, iter: 4 , pairs changed 0
iteration number: 5
fullSet, iter: 5 , pairs changed 0
iteration number: 6
fullSet, iter: 6 , pairs changed 0
iteration number: 7
fullSet, iter: 7 , pairs changed 0
iteration number: 8
fullSet, iter: 8 , pairs changed 0
iteration number: 9
fullSet, iter: 9 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 0
iteration number: 3
fullSet, iter: 3 , pairs changed 0
iteration number: 4
fullSet, iter: 4 , pairs changed 0
iteration number: 5
fullSet, iter: 5 , pairs changed 0
iteration number: 6
fullSet, iter: 6 , pairs changed 1
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 0
iteration number: 3
fullSet, iter: 3 , pairs changed 3
iteration number: 0
fullSet, iter: 0 , pairs changed 0
iteration number: 1
fullSet, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 0
iteration number: 3
fullSet, iter: 3 , pairs changed 0
iteration number: 4
fullSet, iter: 4 , pairs changed 0
iteration number: 5
fullSet, iter: 5 , pairs changed 0
iteration number: 6
fullSet, iter: 6 , pairs changed 0
iteration number: 7
fullSet, iter: 7 , pairs changed 0
iteration number: 8
fullSet, iter: 8 , pairs changed 0
iteration number: 9
fullSet, iter: 9 , pairs changed 0
iteration number: 10

png

1
2
3
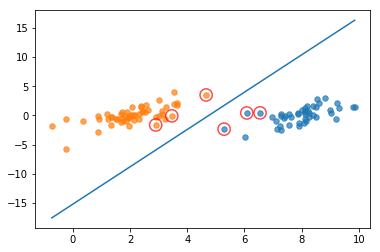
b, alphas = smoP(data_arr,label_arr,0.6,0.001,40)
ws = calc_ws(alphas,data_arr,label_arr)
showClassifer(data_arr,ws,b)
fullSet, iter: 0 , pairs changed 6
iteration number: 1
non-bound, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 0
iteration number: 3

png

1
2
3
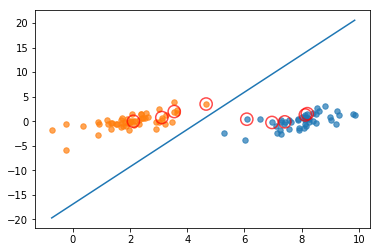
b, alphas = smoP(data_arr,label_arr,0.01,0.001,40)
ws = calc_ws(alphas,data_arr,label_arr)
showClassifer(data_arr,ws,b)
fullSet, iter: 0 , pairs changed 10
iteration number: 1
non-bound, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 0
iteration number: 3

png

1
2
3
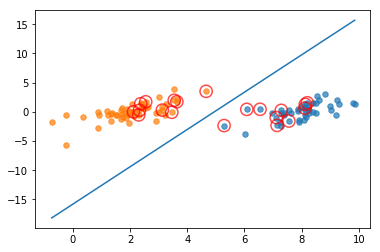
b, alphas = smoP(data_arr,label_arr,55,0.001,40)
ws = calc_ws(alphas,data_arr,label_arr)
showClassifer(data_arr,ws,b)
fullSet, iter: 0 , pairs changed 8
iteration number: 1
non-bound, iter: 1 , pairs changed 0
iteration number: 2
fullSet, iter: 2 , pairs changed 0
iteration number: 3

png

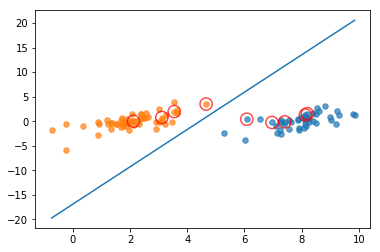
核函数
径向基核函数
$k(x,y) = exp(\frac{-||x -y||^2}{2\sigma^2})$

自变量为向量，可以计算自变量相对于(0,0)或者其他的向量距离

$\sigma$为到达率(reach)或者函数值跌落到0的速度参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#转换核函数
def kernelTrans(X,A,kTup):
    """X为整个数据集，A为其中一行，计算A行和整个数据集的核函数内积
        如果是线性，的则直接得到x * xi^T
    """
    m,n = shape(X)
    K = np.mat(np.zeros((m,1)))
    if kTup[0] == 'lin':
        K = X * A.T #数据集i列的内积 (m,n) * (n,1) => (m,1)
    elif kTup[0] == 'rbf':
        for j in range(m): #读取第j行的值,x 
            deltaRow = X[j,:]  -A #j行减去i行的差，x-y (1,n)
            K[j] = deltaRow * deltaRow.T #得到L2反数
        K = exp(K / (-1 * kTup[1] ** 2)) #各值计算得到和函数的值,k有m行
    else:
        raise NameError('Houston we have a problem --That Kernel is not recognized')
    return K


class optStructk:
    def __init__(self,dataMatIn, classLabels, C, toler, kTup):  # Initialize the structure with the parameters 
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = shape(dataMatIn)[0]
        self.alphas = mat(zeros((self.m,1)))
        self.b = 0
        self.eCache = mat(zeros((self.m,2))) #first column is valid flag
        #K为i,j的内积
        self.K = mat(zeros((self.m,self.m)))
        for i in range(self.m):
            #得到第i列的值即y
            self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#修改用到核函数的辅助函数
def calcEk(oS, k):
    fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)
    Ek = fXk - float(oS.labelMat[k])
    return Ek
    
def innerLk(i, oS):
    Ei = calcEk(oS, i)
    if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
        j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand
        alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
        if (oS.labelMat[i] != oS.labelMat[j]):
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L==H: 
            #print("L==H"); 
            return 0
        eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #changed for kernel
        if eta >= 0: 
            #print("eta>=0"); 
            return 0
        oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
        oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
        updateEk(oS, j) #added this for the Ecache
        if (abs(oS.alphas[j] - alphaJold) < 0.00001):
            #print("j not moving enough"); 
            return 0
        oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j
        updateEk(oS, i) #added this for the Ecache                    #the update is in the oppostie direction
        b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
        b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
        if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
        elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
        else: oS.b = (b1 + b2)/2.0
        return 1
    else: return 0
def smoPk(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)):    #full Platt SMO
    oS = optStructk(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)
    iter = 0
    entireSet = True; alphaPairsChanged = 0
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged = 0
        if entireSet:   #go over all
            for i in range(oS.m):        
                alphaPairsChanged += innerLk(i,oS)
                #print("fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
            print("fullSet, iter: %d , pairs changed %d" % (iter,alphaPairsChanged))
            iter += 1
        else:#go over non-bound (railed) alphas
            nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            for i in nonBoundIs:
                alphaPairsChanged += innerLk(i,oS)
                #print("non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
            print("non-bound, iter: %d , pairs changed %d" % (iter,alphaPairsChanged))
            iter += 1
        if entireSet: entireSet = False #toggle entire set loop
        elif (alphaPairsChanged == 0): entireSet = True  
        print("iteration number: %d" % iter)
    return oS.b,oS.alphas

$f(x) = \sum\limits_{i=1}^m\alpha_i^*y_iK(x\cdot x_i) + b^*$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def testRbf(k1=1.3):
    dataArr,labelArr = loadDataset('../../Downloads/machinelearninginaction/Ch06/testSetRBF.txt')
    b,alphas = smoPk(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1)) #C=200 important
    datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
    #得到支持向量的索引
    svInd=nonzero(alphas.A>0)[0] #[0]是因为alphas是一个mat，[1]是都是0的array
    sVs=datMat[svInd] #get matrix of only support vectors
    labelSV = labelMat[svInd];
    print("there are %d Support Vectors" % shape(sVs)[0])
    m,n = shape(datMat)
    errorCount = 0
    for i in range(m):
        #除了支持向量的a都是0，只需要计算支持向量的核函数
        kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1)) #计算支持向量与数据的和函数，(shape(sVs)[0],1)     
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b #(1,i) * (i,1) =>(1,1)
        if sign(predict)!=sign(labelArr[i]): errorCount += 1
    print("the training error rate is: %f" % (float(errorCount)/m))
    dataArr,labelArr = loadDataset('../../Downloads/machinelearninginaction/Ch06/testSetRBF2.txt')
    errorCount = 0
    datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
    m,n = shape(datMat)
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if sign(predict)!=sign(labelArr[i]): errorCount += 1    
    print("the test error rate is: %f" % (float(errorCount)/m) )
1
testRbf()
fullSet, iter: 0 , pairs changed 30
iteration number: 1
non-bound, iter: 1 , pairs changed 5
iteration number: 2
non-bound, iter: 2 , pairs changed 2
iteration number: 3
non-bound, iter: 3 , pairs changed 0
iteration number: 4
fullSet, iter: 4 , pairs changed 0
iteration number: 5
there are 29 Support Vectors
the training error rate is: 0.130000
the test error rate is: 0.150000

$\sigma$ 如果太小，会得到很多支持向量，因为各支持向量的影响会变小，所以需要更多支持向量，但是容易过拟合

$\sigma $如果过大，则支持向量变小，容易欠拟合

手写识别问题回顾

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
def img2vector(filename):
    returnVect = zeros((1,1024))
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVect[0,32*i+j] = int(lineStr[j])
    return returnVect

def loadImages(dirName):
    from os import listdir
    hwLabels = []
    trainingFileList = listdir(dirName)           #load the training set
    m = len(trainingFileList)
    trainingMat = zeros((m,1024))
    for i in range(m):
        fileNameStr = trainingFileList[i]
        fileStr = fileNameStr.split('.')[0]     #take off .txt
        classNumStr = int(fileStr.split('_')[0])
        if classNumStr == 9: hwLabels.append(-1)
        else: hwLabels.append(1)
        trainingMat[i,:] = img2vector('%s/%s' % (dirName, fileNameStr))
    return trainingMat, hwLabels    

def testDigits(kTup=('rbf', 10)):
    dataArr,labelArr = loadImages('../../Downloads/machinelearninginaction/Ch06/digits/trainingDigits')
    b,alphas = smoPk(dataArr, labelArr, 200, 0.0001, 10000, kTup)
    datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
    svInd=nonzero(alphas.A>0)[0]
    sVs=datMat[svInd] 
    labelSV = labelMat[svInd];
    print("there are %d Support Vectors" % shape(sVs)[0])
    m,n = shape(datMat)
    errorCount = 0
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if sign(predict)!=sign(labelArr[i]): errorCount += 1
    print("the training error rate is: %f" % (float(errorCount)/m))
    dataArr,labelArr = loadImages('../../Downloads/machinelearninginaction/Ch06/digits/testDigits')
    errorCount = 0
    datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
    m,n = shape(datMat)
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if sign(predict)!=sign(labelArr[i]): errorCount += 1    
    print("the test error rate is: %f" % (float(errorCount)/m))
1
testDigits()
fullSet, iter: 0 , pairs changed 104
iteration number: 1
non-bound, iter: 1 , pairs changed 11
iteration number: 2
non-bound, iter: 2 , pairs changed 0
iteration number: 3
fullSet, iter: 3 , pairs changed 0
iteration number: 4
there are 115 Support Vectors
the training error rate is: 0.000000
the test error rate is: 0.016129